Weak Diffie-Hellman Parameters

21 Jun 2016 » security, math, python

Not a long time ago a friend of mine told me that the nginx at duckpond.ch is using 1024 bit standard DH parameters.

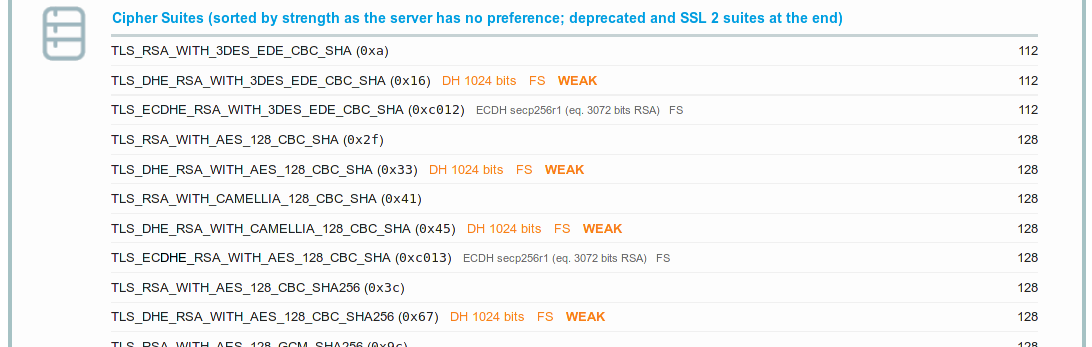ssl lab-weak ciphers SSL-Lab: weak key negotiation because of standard DH parameters

Eww, after being at the 32c3-logjam talk I should have known better. So let’s have some fun with DH before changing the parameters to something (hopefully) more secure.

Openssl is fat and messy and I don’t particularly like their man pages ¹. This is why I started reading some blogs. I really like the step by step instructions by steven gordon. Following steven’s blog I defined a plan of action:

Extracting parameters \(g, p\) from duckpond.ch.
Generate private random \(r_{c}\) for these parameters.
Perform a DH-key agreement with duckpond.ch using s_client with the just generated private random \(r_{c}\). Our goal is to agree with duckpond on a pre-master secret \(k_{0}\) with: \begin{equation} k_{0} \equiv g^{r_{c} r_{s}} \pmod{p} \end{equation}
Derive the master secret \(k\) from the calculated pre-master secret \(k_{0}\). \begin{equation} k = kdf(k_{0}) \end{equation}
Try to solve \(log_{g}(g^{r_{c}}) \pmod{p}\) in order to get \(r_{c}\) back.

Extracting parameters

Extracting the parameters from duckpond.ch: ²

In : g = 2 
In : p = 0xbbbc2dcad84674907c43fcf580e9cfdbd958a3f568b42d4b08eed4eb0fb3504c6c030276e710800c5ccbbaa8922614c5beeca565a5fdf1d287a2bc049be6778060e91a92a757e3048f68b076f7d36cc8f29ba5df81dc2ca725ece66270cc9a5035d8ceceef9ea0274a63ab1e58fafd4988d0f65d146757da071df045cfe16b9b

checking that I got the whole 1024-bit prime:

In : log(p)/log(2)
Out: 1023.552554397631

Openssl works with a PEM ³ encoded parameters file. Thus we’ve to pack our prime modulo \(p\) and generator \(g\) in an ASN.1 encoded representation. I could not find a way using Openssl to generate a arbitrary parameters file. This means I had to “reverse” ⁴ the PEM data, using Lapo Luchini’s ASN.1 decoder. It’s not rocket science; the following python script generates a PEM ⁵ for an arbitrary \(p\) (first argument), \(g\) (second argument) combination.

#!/usr/bin/env python
import sys
import base64
import textwrap
from math import *

from pyasn1.type import univ
from pyasn1.codec.ber import encoder

def usage():
    """print usage"""
    print(  """Usage: {} prime generator
    NOTE: Numbers in hexadecimal""".format(sys.argv[0]))
    sys.exit(-1)

PEM_LINE_LENGTH = 64 - 1 # -1 because of \n
def pem_lines(m):
    """Yield successive lines of PEM body for bytearray m"""
    m = base64.b64encode(m).decode('ascii')
    for i in range(0, len(m), PEM_LINE_LENGTH):
        yield m[i:i+PEM_LINE_LENGTH]

if len(sys.argv) != 3:
    usage()

(_, prime, generator) = sys.argv
prime = int(prime, 16)
generator = int(generator,16)

m = encoder.encode(
        univ.Sequence().setComponents(
            univ.Integer(prime),
            univ.Integer(generator)
        )
    )

print('-----BEGIN DH PARAMETERS-----')
[print(l) for l in pem_lines(m)]
print('-----END DH PARAMETERS-----')

Using the script:

$ ./pem-dhgen.py 0x2 0xbbbc2dcad84674907c43fcf580e9cfdbd958a3f568b42d4b08eed4eb0fb3504c6c030276e710800c5ccbbaa8922614c5beeca565a5fdf1d287a2bc049be6778060e91a92a757e3048f68b076f7d36cc8f29ba5df81dc2ca725ece66270cc9a5035d8ceceef9ea0274a63ab1e58fafd4988d0f65d146757da071df045cfe16b9b
-----BEGIN DH PARAMETERS-----
MIGHAgECAoGBALu8LcrYRnSQfEP89YDpz9vZWKP1aLQtSwju1OsPs1BMbAMCduc
QgAxcy7qokiYUxb7spWWl/fHSh6K8BJvmd4Bg6RqSp1fjBI9osHb302zI8pul34
HcLKcl7OZicMyaUDXYzs7vnqAnSmOrHlj6/UmI0PZdFGdX2gcd8EXP4Wub
-----END DH PARAMETERS-----

Generate \(r_{c}\)

The generated PEM can be used for Openssl’s genpkey command ⁶.

$ openssl genpkey -paramfile dhp.pem -text
-----BEGIN PRIVATE KEY-----
MIIBIQIBADCBlQYJKoZIhvcNAQMBMIGHAoGBALu8LcrYRnSQfEP89YDpz9vZWKP1
aLQtSwju1OsPs1BMbAMCducQgAxcy7qokiYUxb7spWWl/fHSh6K8BJvmd4Bg6RqS
p1fjBI9osHb302zI8pul34HcLKcl7OZicMyaUDXYzs7vnqAnSmOrHlj6/UmI0PZd
FGdX2gcd8EXP4WubAgECBIGDAoGAfDxqaNChsZaQuJ9W/o/Jh0J6HmaOOrrHl4d9
W5rRR4XsT8IVIeuD3fQo6TXWn5y8ULngmVs+WiKLZRtO35N4Uu1z45bFutdTcuu/
rMbm5WVknaHH/6K5ygBRQD4d0FW9KxywwFnPGyD3lBlyGpqUgA/EDF+02Il+Y5ho
Qpi8VHA=
-----END PRIVATE KEY-----
DH Private-Key: (1024 bit)
    private-key:
        7c:3c:6a:68:d0:a1:b1:96:90:b8:9f:56:fe:8f:c9:
        87:42:7a:1e:66:8e:3a:ba:c7:97:87:7d:5b:9a:d1:
        47:85:ec:4f:c2:15:21:eb:83:dd:f4:28:e9:35:d6:
        9f:9c:bc:50:b9:e0:99:5b:3e:5a:22:8b:65:1b:4e:
        df:93:78:52:ed:73:e3:96:c5:ba:d7:53:72:eb:bf:
        ac:c6:e6:e5:65:64:9d:a1:c7:ff:a2:b9:ca:00:51:
        40:3e:1d:d0:55:bd:2b:1c:b0:c0:59:cf:1b:20:f7:
        94:19:72:1a:9a:94:80:0f:c4:0c:5f:b4:d8:89:7e:
        63:98:68:42:98:bc:54:70
    public-key:
        5c:59:23:8c:0b:09:78:f3:8f:db:f0:15:c1:2d:da:
        e1:f7:ca:a5:8c:42:e0:ff:29:da:33:ae:89:6d:cb:
        78:d4:3e:0d:11:79:5c:82:f2:8d:27:bb:ca:12:fb:
        22:ef:de:48:c3:00:0d:e7:a3:0d:3e:61:3d:0d:d8:
        82:bb:16:d7:73:94:f3:1c:54:39:de:cd:d9:c9:38:
        55:95:d3:d0:b5:aa:9f:66:01:56:29:00:6b:04:bb:
        22:a6:66:16:51:d1:44:32:60:04:5a:2b:7b:c5:a8:
        70:25:2d:40:07:d3:46:fe:62:1f:5d:2c:bb:24:c9:
        50:7a:54:d3:a9:e2:62:18
    prime:
        00:bb:bc:2d:ca:d8:46:74:90:7c:43:fc:f5:80:e9:
        cf:db:d9:58:a3:f5:68:b4:2d:4b:08:ee:d4:eb:0f:
        b3:50:4c:6c:03:02:76:e7:10:80:0c:5c:cb:ba:a8:
        92:26:14:c5:be:ec:a5:65:a5:fd:f1:d2:87:a2:bc:
        04:9b:e6:77:80:60:e9:1a:92:a7:57:e3:04:8f:68:
        b0:76:f7:d3:6c:c8:f2:9b:a5:df:81:dc:2c:a7:25:
        ec:e6:62:70:cc:9a:50:35:d8:ce:ce:ef:9e:a0:27:
        4a:63:ab:1e:58:fa:fd:49:88:d0:f6:5d:14:67:57:
        da:07:1d:f0:45:cf:e1:6b:9b
    generator: 2 (0x2)

Well, that was easy…

Key agreement

Then I used s_client with the just generated private key and recorded the ssl-handshake: ⁷

$ openssl s_client -connect duckpond.ch:443 -cipher DHE-RSA-AES256-SHA256 -key dhkey.pem 

[...]

---
New, TLSv1/SSLv3, Cipher is DHE-RSA-AES256-SHA256
Server public key is 4096 bit
Secure Renegotiation IS supported
Compression: NONE
Expansion: NONE
No ALPN negotiated
SSL-Session:
    Protocol  : TLSv1.2
    Cipher    : DHE-RSA-AES256-SHA256
    Session-ID: A137EBD4BC7E0407C9EE1C2C3DFAEF372B582F6434B6ED5A18C5121293F14484
    Session-ID-ctx: 
    Master-Key: DABAC095DD28532DF643F4BA7476D194851E64F75BCE4C5EADA2906B702B1F758BB15FED4A37DB2682791D9ACA629DDA
    Key-Arg   : None
    PSK identity: None
    PSK identity hint: None

[...]

After this I extracted the transmitted \(g^{r_{c}}\) from the ssl-handshake:

In : gr_c = 0xac5b13ac2d295e8779d1beca26c06f54071d804dd82914160941732f6252875ac61704b925f2e540fead8ef29cc678604cf060f49ca9b5008aa5763ffcf0cced3271000c3ecf7b089e05dd506a9ca9e438c75db80da2a93c6081a5412

and realized that I fucked up. Ephemeral DH (DHE) uses a new \(r_{c}\) for every connection. Which is a good thing to do, but for now very annoying. DHE makes it hard to reproduce results. Attaching a debugger quickly revealed that Openssl does load the provided DH-parameters but is not using them once the Client Key Exchange-message is generated. So I patched Openssl’s crypto/dh/dh_key.c:generate_key() and made it always return the first loaded key ⁸. The first loaded key is the one we provide via the ‘-key’ parameter:

diff --git a/crypto/dh/dh_key.c b/crypto/dh/dh_key.c
index 9b79f39..2c22b46 100644
--- a/crypto/dh/dh_key.c
+++ b/crypto/dh/dh_key.c
@@ -70,6 +70,7 @@ static int generate_key(DH *dh)
     BN_CTX *ctx;
     BN_MONT_CTX *mont = NULL;
     BIGNUM *pub_key = NULL, *priv_key = NULL;
+    static DH *static_dh;
 
     ctx = BN_CTX_new();
     if (ctx == NULL)
@@ -145,6 +146,12 @@ static int generate_key(DH *dh)
     if (priv_key != dh->priv_key)
         BN_free(priv_key);
     BN_CTX_free(ctx);
+    // hack: always reuse same dh parameters
+    if(static_dh == NULL){
+        static_dh = dh;
+    }else{
+        (*dh) = (*static_dh);
+    }
     return (ok);
 }

Re-running the ssl-handshake2 using the patched Openssl version:

$ openssl s_client -connect duckpond.ch:443 -cipher DHE-RSA-AES256-SHA256 -key dhkey.pem 

[...]

---
New, TLSv1.2, Cipher is DHE-RSA-AES256-SHA256
Server public key is 4096 bit
Secure Renegotiation IS supported
Compression: NONE
Expansion: NONE
No ALPN negotiated
SSL-Session:
    Protocol  : TLSv1.2
    Cipher    : DHE-RSA-AES256-SHA256
    Session-ID: 2D9161954D7998884AC496BE16085C7200D36773B83C97746D50B756FF7F3F2B
    Session-ID-ctx: 
    Master-Key: 403247E9625BE70E2AC4076297B48A18178696404FC7FFCD924ECAA5628FDBA049DFBD4170F65ACBC6A84AA18696144A
    PSK identity: None
    PSK identity hint: None

[...]

And extracting the \(g^{r_{c}}\) from the new ssl-handshake2:

g_rc = 0x5c59238c0b0978f38fdbf015c12ddae1f7caa58c42e0ff29da33ae896dcb78d43e0d11795c82f28d27bbca12fb22efde48c3000de7a30d3e613d0dd882bb16d77394f31c5439decdd9c9385595d3d0b5aa9f66015629006b04bb22a6661651d1443260045a2b7bc5a870252d4007d346fe621f5d2cbb24c9507a54d3a9e26218

Finally the \(g^{r_{c}}\) is the same as the just generated public-key. Which means the we should be able to compute the \(g^{r_{c}}\) using the known private key \(r_{c}\):

In : r_c = 0x7c3c6a68d0a1b19690b89f56fe8fc987427a1e668e3abac797877d5b9ad14785ec4fc21521eb83ddf428e935d69f9cbc50b9e0995b3e5a228b651b4edf937852ed73e396c5bad75372ebbfacc6e6e565649da1c7ffa2b9ca0051403e1dd055bd2b1cb0c059cf1b20f79419721a9a94800fc40c5fb4d8897e6398684298bc5470
In : pow(g, r_c, p) == g_rc
Out: True

Yayy! From here it should be straight forward to calculate the pre-master secret \(k_{0}\).

\begin{equation} k_{0} \equiv g^{r_{c} r_{s}} \equiv g^{r_{s}^{r_{c}}} \pmod{p} \end{equation}

The only thing we need for this is the server public key \(g^{r_{s}}\) which is easy to extract from the ssl-handshake2:

In : g_rs = 0x3f2be9298aa84d6889dcfbd1a0bb0788a440b81f5b5b5d948174c6a1daf729d8f760ecf5363cdbee460ceee8f8b64d8a1710c61a9a8b9f043570e6a17ce0846f1af6a215dd4c5dd2e567547345cd9b9ef24af8791060f2e7451f11735f64d3b80d1d2253587ca3c5676ed3f1c84e96d32d9766607811a9996e802cacc4b97f05
In : k0 = pow(g_rs, r_c, p)

Now I’m in perfect shape for step 4 and 5 which I’ll do in a follow-up.

If somebody can point out a good cheat-sheet I’d be soooo happy. ↩
By capturing an ssl-handshake. ↩
I’ve no idea what this has to do with mail. ↩
The ASN.1 standard is even more cumbersome than Openssl manpages. ↩
Append it to all the MAIL! ↩
So that you can send it to your friends via mail. ↩
Yes, I restarted the web server and client after doing this. ↩
Don’t do this at home. ↩

Support Binary File Objects with pandas.DataFrame.to_csv (Categories: python, bash)
TOFU for Containers (Categories: tls-tofu, git-sync-mirror, kamikaze, security)
Pdml2flow 5.0 (Categories: pdml2flow, networking, python)
Broken One-time pad 2 (Categories: security, math, python)
Clusteranalyse von Malware basierend auf Installationsgraphen (Categories: security, math)
Broken One-time pad [Solved] (Categories: security, math, python)

Extracting parameters

Generate \(r_{c}\)

Key agreement

Related Posts